Reading list:
- https://jonathan-hui.medium.com/speech-recognition-phonetics-d761ea1710c0
- https://jonathan-hui.medium.com/speech-recognition-gmm-hmm-8bb5eff8b196
- https://jonathan-hui.medium.com/speech-recognition-acoustic-lexicon-language-model-aacac0462639
- https://jonathan-hui.medium.com/speech-recognition-asr-decoding-f152aebed779
- https://jonathan-hui.medium.com/speech-recognition-weighted-finite-state-transducers-wfst-a4ece08a89b7
- https://jonathan-hui.medium.com/speech-recognition-asr-model-training-90ed50d93615
Example Implementations:
The statistical approach tries to model the most probable word sequence given the audio signals.
Given
Word sequence: Acoustic observations:
We can write it as the following equation:
(using Bayes Theorem we can simplify it to)
(since we are maximizing w and it does not depend on X, we can simplify it a bit more)
We want to find the word sequence W that maximizes P(X|W). But instead of predicting the word sequence that maximizes P(W|X) we want to find the word sequence that maximizes the probability of the audio frame given the word sequence, P(X|W) and the probability of the word sequence occurring. This is supposedly more tractable.
P(X|W) is the acoustic model, it concerned with predicting how likely an audio signal is given a word sequence. P(W) is the language model, it is concerned with predicting how likely a sequence of words. For example, “black cry grass” is less likely than “green cut grass”.
Now you might say, as I once did how do we get the word sequence that maximizes P(X|W), given that we observed X and want to predict W, and how do we get the Probability of a thing we don’t even know, P(W).
Be patient :)
Till now we said that we want predict a sequence of words given an input audio. And this is what we do, but inside our model we do not use words directly we instead use phones as they are more fundamental (denser representation) in speech. We will convert our phones to words at the end using a pronunciation table. In our notations we will still use W but keep in mind that we mean phones.
In our journey to transcribe audio signals to text, we first need to convert them into a usable format. We do this by extracting the Mel-Frequency Cepstral Coefficients (MFCC) for a specific frame of the audio signal. For example we can extract the MFCC an audio clip with 39 coefficient for an audio frame of length 25 ms every 10 ms, the following diagram illustrates this:
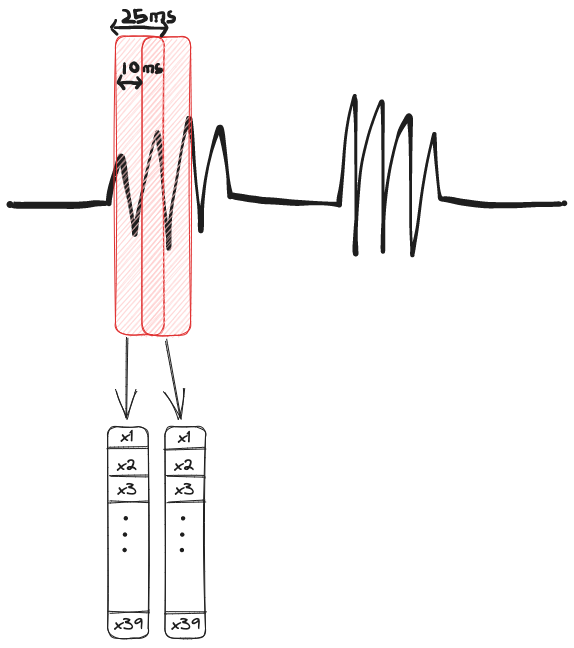
Now that we have our X in a usable format, we can start building our acoustic model, that is P(X|W). But before doing so we need to introduce a few key concepts: Gaussian mixture models, Markov chains and Hidden Markov models.
Given a phone we want to estimate the probability of observing an audio feature. We can model this by a gaussian distribution for each possible phone. To extend this concept to 39 coefficient, we can use multivariate gaussian distribution. To account for variations in phones (speed, speakers, intonations, etc.) we can use gaussian mixture models, which are a probabilistic model for representing normally distributed subpopulations within an overall populations. Each phone will have with it a Gaussian mixture model, where when we input the extracted features of the audio signal we get a probability that it belonged to that phone.
Now that we capture the acoustic feature of speech with our GMM. We need a way to capture the temporal structure of our speech. To do this let’s introduce Markov chains and Hidden Markov Models.
Markov chains are a way to describe a system with states and transitions to states. An important property of Markov chains is that the next state only depends on the current state and not the sequence of events that preceded it. This makes it much easier to handle.