2025-05-26 14:45

(Github)

Building a High-Performance GEMM Kernel

In this blog, we will implement a general purpose matrix multiplication program and optimize the sh** out it, explaining each optimization technique along the way. We will not seek any algorithmic savings, although those are often more important.

Measuring performance

There are several ways we can measure performance. The most straightforward one is to measure how long the program takes and how many operations per second it performs. This is good enough for our use case because we only care about how these metrics have improved from one implementation to the next.

Execution Time and GFLOPS

---

Execution time:

• $t$ : execution time in seconds
• $\text{start}$: program start time
• $\text{end}$: program end time

$$t=\text{end}-\text{start}$$

To make sure we have consistent readings, we average out the execution time over multiple runs.

$$\bar{t}=\frac{1}{n}\sum _{i=1}^n{t}_i$$

We would want to minimize $\bar{t}$.

---

We define a matrix multiplication:

$$C=A\cdot B$$

Where:

• $A\in {\mathbb{R}}^{M\times K}$
• $B\in {\mathbb{R}}^{K\times N}$
• $C\in {\mathbb{R}}^{M\times N}$

Each element of $C$ is computed as:

$$C_{i,j}=\sum _{k=1}^K{A}_{i,k}\cdot B_{k,j}$$

The total number of floating point operations in the inner loop is 2 (one add and one multiply). This would be performed $M\ast N\ast K$ times. Thus the total number of (10^9) floating point operations per second is:

$$\text{GFLOPS}=\frac{2\cdot M\cdot N\cdot K}{t\cdot 10^9}$$

We would want to maximize $\text{GFLOPS}$.

Initial Implementation

void gemm_naive(const float* A, const float* B, float* C, int M, int N, int K) {
    // C[M][N] = A[M][K] * B[K][N]
    for (int i = 0; i < M; ++i)
        for (int j = 0; j < N; ++j) {
            for (int k = 0; k < K; ++k)
                C[i * N + j] += A[i * K + k] * B[k * N + j];
        }
}

Our simple implementation performs a matrix multiplication using three for loops.

Measuring it’s performance we observe the following results.

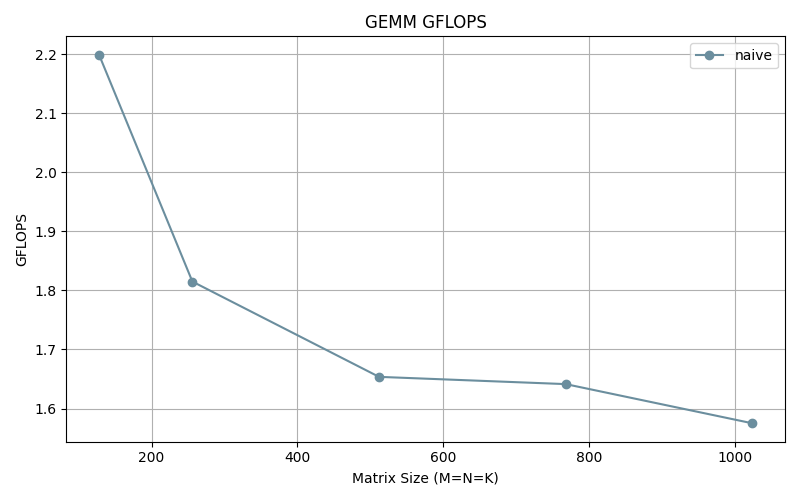
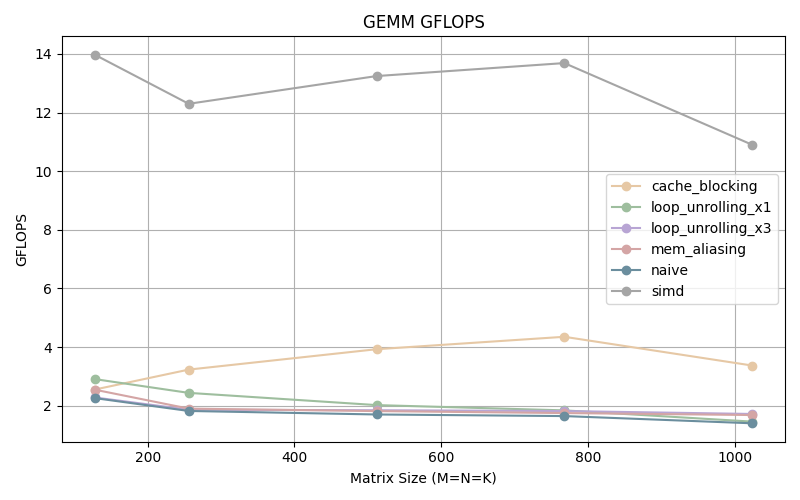
We can observe that the GFLOPS gradually descends as the matrix size increases. This can be explained by the fact that more cache misses are occurring as size increases (because the data can’t fit in the cache anymore) resulting in more of data movements (as data is fetched from memory) which slows down our program.

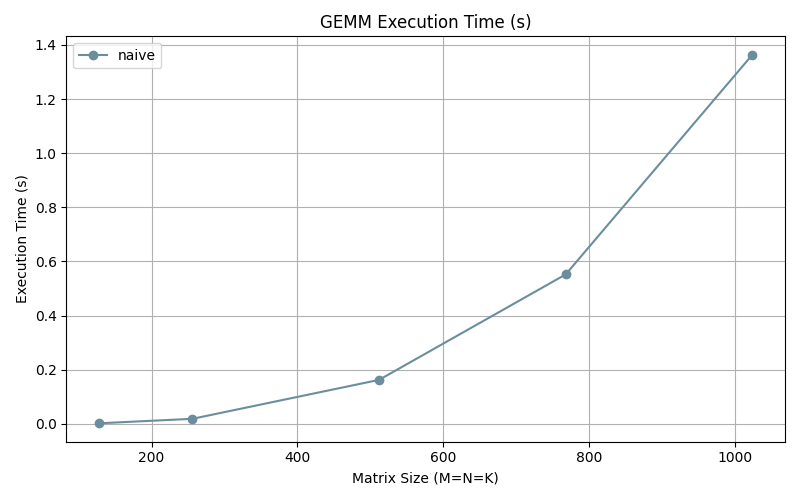
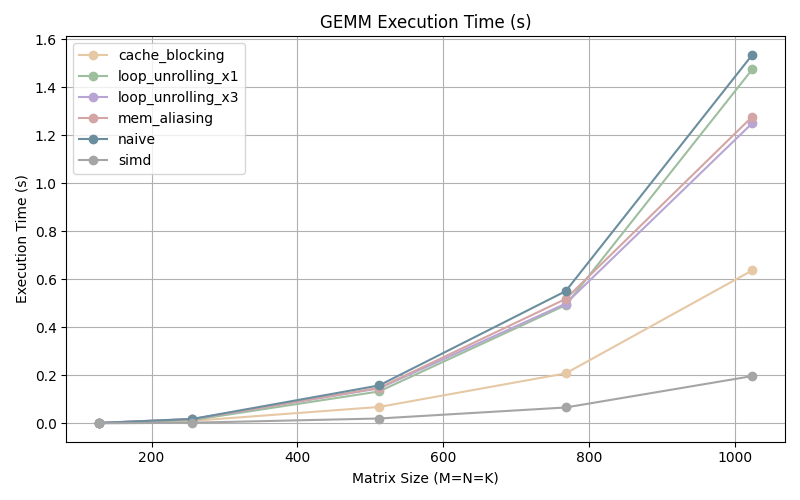
The execution time grows exponentially with size as expected.

Basic Optimization

Optimizing Compilers

Modern compilers employ optimization techniques such as code selection and ordering, dead code elimination, register allocation and eliminating minor inefficiencies. Although they are helpful, there are limitations to how aggressively it can optimize our code because it operates under fundamental constraints (no change in program behavior) and limited context (analysis performed only within procedures and based only on static information).

When in doubt the compiler must be conservative.

One such optimization blockers is the potential for memory aliasing.

Memory Aliasing

If we take a closer look at the assembly code that corresponds to C[i * N + j] += A[i * K + k] * B[k * N + j] we can see the following in the third inner loop:

        addss   %xmm0, %xmm1
        movss   %xmm1, 0(%r13)

The concerning line is the second one because It means that we update C[i * N + j] on every iteration. We are performing an unnecessary operation on each iteration.

This might seem like an obvious job for the compiler to optimize as we do not need to update the memory only once and not on every iteration. But the compiler must consider the possibility that A and/or B point to the same memory as C. If that were the case we are changing the value of the elements on each iteration thus need to update the memory.

The compiler cannot perfectly detect if two pointers point to the same thing because the value of the pointers can be dependent on runtime behavior, and in the general case determining wether aliasing occurred is undecidable because of the halting problem.

Compilers assume aliasing is possible unless they can prove it’s not, which is possible only in very simple cases. They take the conservative route and update the memory on each iterations.

One way we can resolve this is by accumulating the sum within the loop and update the memory at end of the iterations.

void gemm_mem_aliasing(const float* A, const float* B, float* C, int M, int N, int K) {
    for (int i = 0; i < M; ++i)
        for (int j = 0; j < N; ++j) {
            float sum = 0.0f;
            for (int k = 0; k < K; ++k)
                sum += A[i * K + k] * B[k * N + j]; //accumulate in sum
            C[i * N + j] = sum;
        }
}

We observe the following improvements:

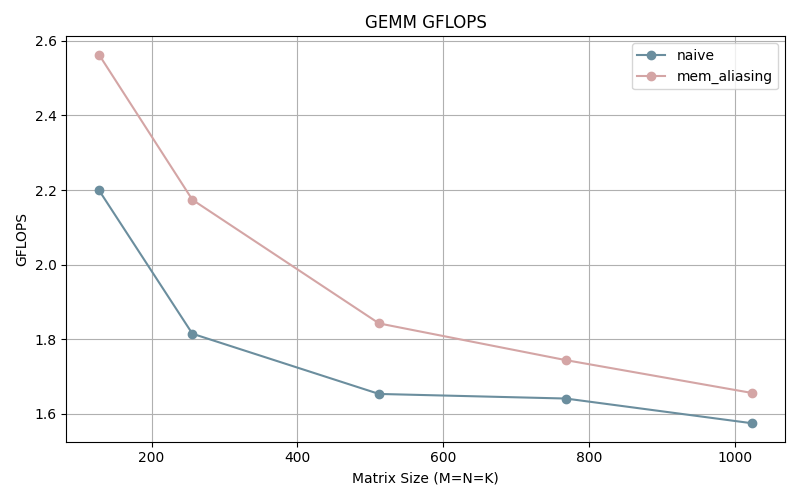
We can observe that we are performing more operations per second.

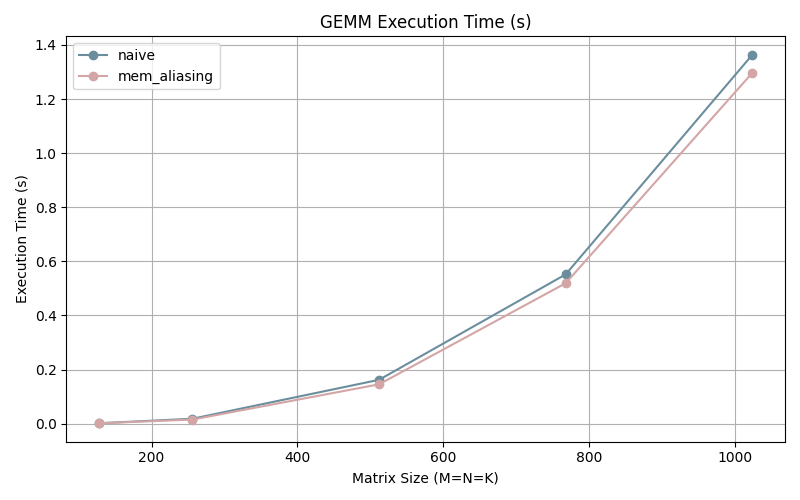
We can also observe that our execution time has decreased. As the matrix grows bigger, our optimization effect becomes clearer.

By accumulating the sum within the loop, we are performing one less instruction per iteration. The less instructions the better (kind of, depends on the instruction).

Loop Unrolling

Modern processors don’t execute instructions one at a time as reading the assembly code of program suggests. Instead they perform instruction level parallelism where complex mechanisms are employed to execute multiple instructions at the same time while presenting a view of a simple sequential instruction execution.

In this model, computation is divided into stages and while one goes through the different stages another can start if they have no dependency.

The following table shows the latency (how many clock cycles an instruction takes), the cycle/issue (the minimum number of cycles between two independent instructions) and the capacity (how many of these operations can be issued simultaneously) for Intel Core i7 Haswell CPUs.

Instruction	Latency	Cycles/Issue	Capacity
Load/Store	4	1	2
Store	4	1	1
Integer Add	1	1	4
Integer Multiply	3	1	1
Integer/Long Divide	3–30	3–30	1
Single/Double FP Multiply	5	1	2
Single/Double FP Add	3	1	1
Single/Double FP Divide	3–15	3–15	1

The assemble code of our inner loop before unrolling

.L4:
        movss   (%rax), %xmm0
        mulss   (%rdx), %xmm0
        addq    $4, %rax
        addq    %rsi, %rdx
        addss   %xmm0, %xmm1
        cmpq    %rax, %rdi
        jne     .L4

and after unrolling

.L4:
        movss   (%rax), %xmm1
        mulss   (%rdx), %xmm1
        addq    $8, %rax
        addss   %xmm1, %xmm0
        movss   -4(%rax), %xmm1
        mulss   (%rdx,%rcx,4), %xmm1
        addq    %rdi, %rdx
        addss   %xmm1, %xmm0
        cmpq    %rax, %r8
        jne     .L4
        movss   %xmm0, (%r11,%r9,4)
        addq    $1, %r9
        addq    $4, %r10
        cmpq    %r9, %rcx
        jne     .L5
        movl    -36(%rsp), %edx

Doing more work in the inner loop would give us optimization gains in two ways:

• Minimizes the number of operation outside of the loop ( testing if loop condition is met/ incrementing)
• Gives the processor an opportunity to rearrange the execution order, and run some of the instructions in parallel.

We can unroll the loop once by adding one more operation in the inner loop. We can further unroll the loop by adding three operations in the inner loop.

void gemm_loop_unrolling_x1(const float* A, const float* B, float* C, int M, int N, int K) {
    for (int i = 0; i < M; ++i)
        for (int j = 0; j < N; ++j) {
            float sum = 0.0f;
            for (int k = 0; k < K; k+=2){
                sum += A[i * K + k] * B[k * N + j];
                sum += A[i * K + k+1] * B[(k+1) * N + j];
            }
                
            C[i * N + j] = sum;
        }
}

void gemm_loop_unrolling_x3(const float* A, const float* B, float* C, int M, int N, int K) {
    for (int i = 0; i < M; ++i)
        for (int j = 0; j < N; ++j) {
            float sum = 0.0f;
            for (int k = 0; k < K; k+=4){
                sum += A[i * K + k] * B[k * N + j];
                sum += A[i * K + k+1] * B[(k+1) * N + j];
                sum += A[i * K + k+2] * B[(k+2) * N + j];
                sum += A[i * K + k+3] * B[(k+3) * N + j];
            }
                
            C[i * N + j] = sum;
        }
}

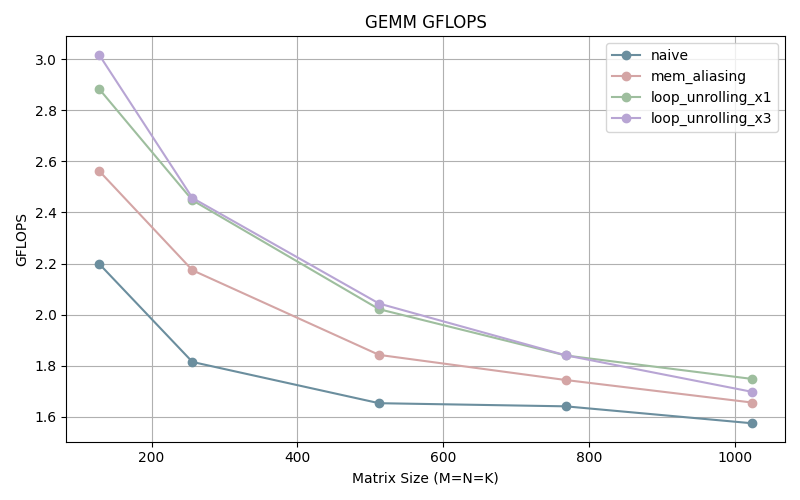
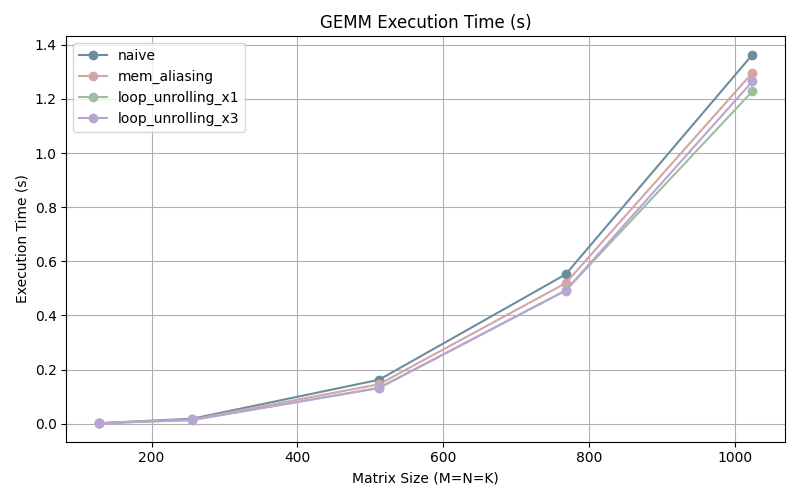
Further optimization gains can be seen by unrolling our loops. Unrolling 3 times is more efficient for smaller matrices but the the difference with the once unrolled program disappears as the size of matrix increases.

We hit a point of diminishing returns when it comes to loop unrolling due to the fact that it requires more and more registers which can lead to exhausting the available CPU registers. When that happens we will be using the memory to store/load variables which has a high performance overhead.

Cache Blocking

Cache Blocking is a technique that minimizes cache misses by working with a subset of the data (blocks) at a time so that it fits in the cache and minimizes expensive reads from memory.

constexpr int BLOCK_M = 64;
constexpr int BLOCK_N = 64;
constexpr int BLOCK_K = 64;
 
void gemm_cache_blocking(const float* A, const float* B, float* C, int M, int N, int K) {
    for (int i0 = 0; i0 < M; i0 += BLOCK_M) {
        for (int j0 = 0; j0 < N; j0 += BLOCK_N) {
            for (int k0 = 0; k0 < K; k0 += BLOCK_K) {
 
                int i_max = std::min(i0 + BLOCK_M, M);
                int j_max = std::min(j0 + BLOCK_N, N);
                int k_max = std::min(k0 + BLOCK_K, K);
 
                for (int i = i0; i < i_max; ++i) {
                    for (int j = j0; j < j_max; ++j) {
                        float sum = C[i * N + j];
                        for (int k = k0; k < k_max; k+=4) {
                            sum += A[i * K + k] * B[k * N + j];
                            sum += A[i * K + k+1] * B[(k+1) * N + j];
                            sum += A[i * K + k+2] * B[(k+2) * N + j];
                            sum += A[i * K + k+3] * B[(k+3) * N + j];
                        }
                        C[i * N + j] = sum;
                    }
                }
            }
        }
    }
}
 

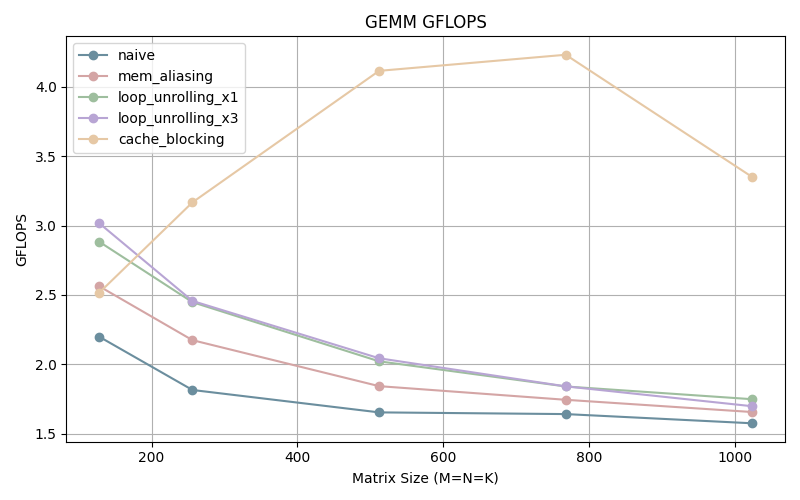
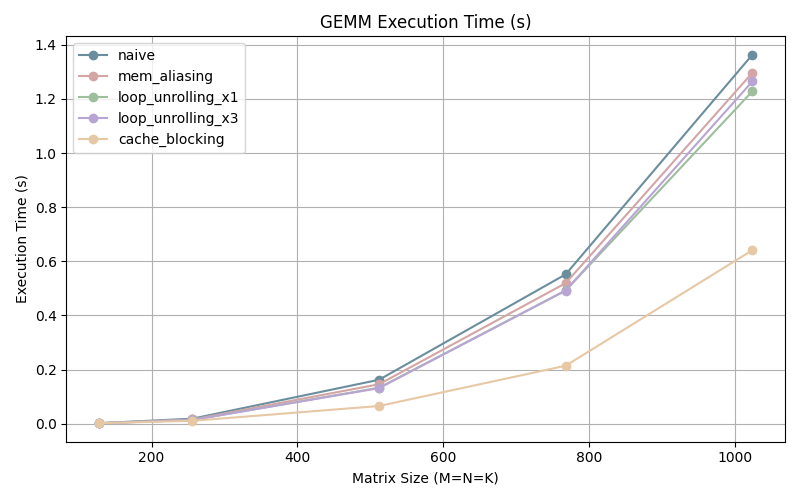
The GFLOPS start out in in the middle of the pack, possibly due to the overhead incurred by the additional operations needed to setup the cache blocking, but as the matrix size increases we can see that we are performing more than twice the amount of operations per second.

This optimization shows us that memory is a big bottleneck in performance. The more we work within the cache, the faster our program is.

SIMD

Single instruction, multiple data (SIMD) operation can perform parallel operation on multiple data elements.

for (int i = i0; i < i_max; ++i) {
    for (int j = j0; j < j_max; j += simd_size) {
        batch_type c_vec = batch_type::load_unaligned(&C[i * N + j]);
        for (int k = k0; k < k_max; k++) {
            batch_type b_vec = batch_type::load_unaligned(&B[k * N + j]);
            float a_scalar = A[i * K + k];
            c_vec = xsimd::fma(batch_type(a_scalar), b_vec, c_vec);
 
	        }
        c_vec.store_unaligned(&C[i * N + j]);
	    }
        // Fallback for leftover columns
        for (int j = j_max - (j_max % simd_size); j < j_max; ++j) {
            float sum = C[i * N + j];
            for (int k = 0; k < K; ++k) {
                sum += A[i * K + k] * B[k * N + j];
            }
            C[i * N + j] = sum;
        }

The inner loop uses Fused Multiply-Add (FMA) operations. FMA combines addition and multiplication in a single instruction which increases throughput (one instruction instead of two), latency (faster than separate multiply + add) , pipeline efficiency (better instruction scheduling), less register pressure (fewer intermediate results). The FMA is vectorized meaning multiple FMA operation can be performed at once.

References

• Computer Systems: A Programmer’s Perspective (3rd Edition)
• Performance x64: Cache Blocking (Matrix Blocking)