Markov Chains

#maths Markov chains are a way to model a system with a sequence of states. The current state can transition to another state according to some probability. The probability of being in a certain state only depends on the previous state. This is represented by the following equation:

$$P(X_{n+1}=x|X_1=x_1,X_2=x_2,\dots ,X_n=x_n)=P(X_{n+1}=x|X_n=x_n)$$

Example:

Let’s try to model the weather with a Markov chain. Our system can be in three different states: sunny, cloudy and rainy days.

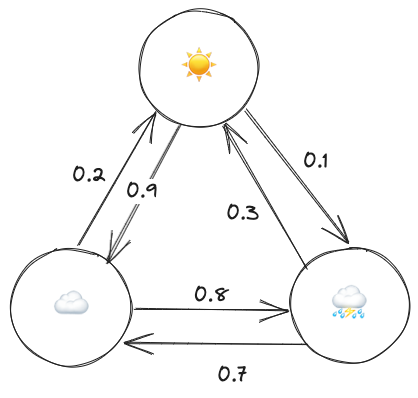Each circle represents a state, and each arrow a transition between states with the number on top of it representing the probability that we transition to a state. Note that the transition probability out of a state always sums to 1. Another important thing to note is that the current state only depends on the previous state. For example let’s say we have the following sequence of days ☀️,☁️, ☀️,☁️, the probability of transitioning to ⛈ only depends on the previous state, that is ☁️. We can thus write:

$$P(X_5=⛈|X_1=☀\stackrel{◯}{R},X_2=☁\stackrel{◯}{R},X_3=☀\stackrel{◯}{R},X_4=☁\stackrel{◯}{R})=P(X_5=⛈|X_4=☁\stackrel{◯}{R}))$$

(Sorry for the inconsistent emojis, blame obsidian)

We can write out all the probabilities in a single matrix. We call this the transition matrix:

$$A=\left[\begin{array}{ccc}0& 0.9& 0.1\\ 0.2& 0& 0.8\\ 0.3& 0.7& 0\end{array}\right]$$

The stationary distribution of a Markov chain is the probability associated with each state that remains unchanged as time progresses. It satisfies:

$$\pi A=\pi$$

In other words $\pi$ is invariant to $A$.

A cool thing to note, is that $\pi$ is the eigenvector associated with the transformation matrix $A$, with the eigenvalue set to 1:

$$\pi A=\lambda \pi$$

References:

• Markov chain
• Markov Chains Clearly Explained! Part - 1
• Eigenvectors and eigenvalues | Chapter 14, Essence of linear algebra
• Stationary Distribution of Markov Chains