Hidden Markov Model

#maths

Code

Hidden Markov Models help us model Markov processes whose observations are the only known parameters.

Let’s say we have a friend, called Nahomie, that lives in a land far far away. One Sunday we call Nahomie, we chat for a few hours and he tells how he’s been feeling for the past few days. He is either sad (😫) or happy (😃). From our years long of friendship, we propose that Nahomie’s mood is chiefly influenced by the weather in his city. He doesn’t believe us, he believes his mood is entirely independent of the weather. How can we prove to our friend that our hunch is correct.

We can model the weather as a Markov Chains and Nahomie’s moods as emissions of the markov process. In our model we have a set of states we can directly observe, the moods, and states that are hidden whose properties we are trying to infer. This is called a Hidden Markov Model (hmm).

We can illustrate our system in the following manner: 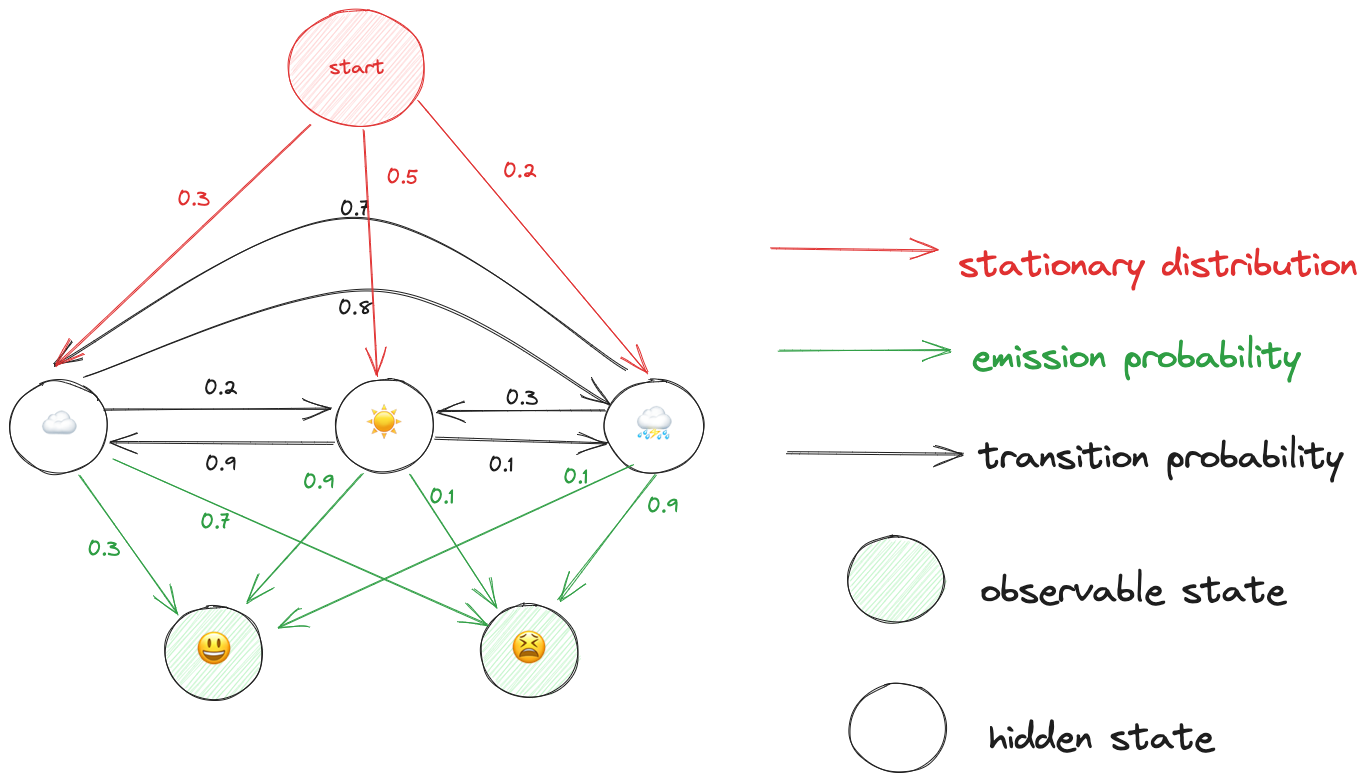A few notes:

• At initial stages, all the probabilities are randomly initialized. That is what we are trying to determine.
• The observable states are the states of the system we can observe, that is Nahomie’s mood.
• The hidden states are the states in the system that we do not directly observe, that is the weather.
• The hidden states form a Markov chain.
• The probability of being in a certain mood given the weather is denoted by emission probability.
• The probability of transitioning from one state to another is given by the transition probability.

From our conversations with Nahomie, we know he has been in the following moods: $O=\{😫,😃,😫\}$.

Using various algorithms, and only our observations $O$, we can answer the following questions.

Can we learn the model’s parameters (transition probabilities, emission probabilities, and stationary distribution) of the Markov chain that lead to these moods?

You can learn the parameters of the Markov Chain using the Baum-Welch Algorithm. This will result in parameters that increase the likelihood of observation $O$. But we can only find a local maximum not a global maximum.

What is the likelihood of observing $O=\{😫,😃,😫\}$ , given our model parameters ?

You can compute the likelihood of an observation using the forward or backward algorithm.

What is the likeliest weather that could have led to O={😫, 😃, 😫}?

You can decode the likeliest sequence of hidden states that led to these moods using the viterbi algorithm.

An implementation of each algorithm mentioned above can be found here.