Baum-Welch Algorithm

#maths The Baum-Welch algorithm helps us find the parameters of a Hidden Markov Model given a sequence of observation.

Given observations $O=o_1,o_2,...,o_N$ and parameters $\lambda =(\pi ,A,B)$ we can find ${\lambda }^{\prime }$ such that $P(O|{\lambda }^{\prime })\le P(O|\lambda )$ using the Baum-Walch algorithm. It only guarantees a local minimum.

Let’s call $\xi (i,j)$ the probability of being in state $S_i$ at time $t$ then state $S_j$ at time $t+1$ given observation $O$ and parameters $\lambda$. We can write it as such:

$\xi (i,j)=P(q_t=S_i,q_{t+1}=S_j|O,\lambda )$

We can illustrate is as:

In the forward algorithm we computed $\alpha$ which captures the probability that we are in state i given the observations that came before it. In the backward algorithm we computed $\beta$ which captures the probability that we will be in the given state knowing what’s going to come in the future.

We have :

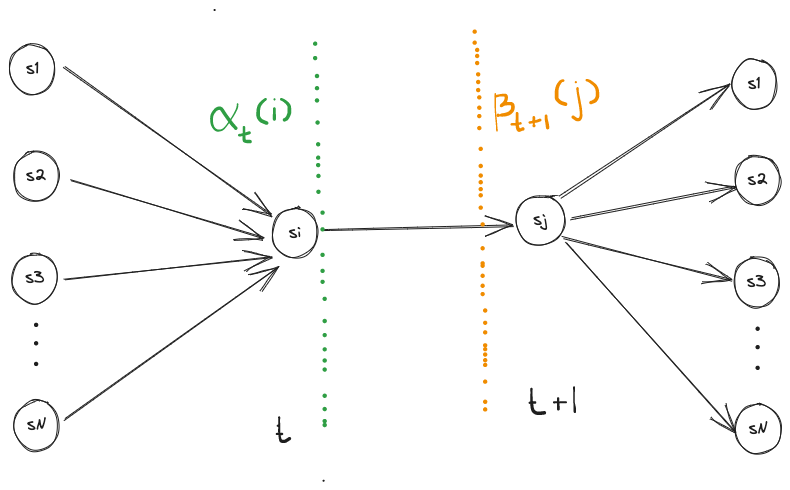
The likelihood that we end up in state $S_i$ at time $t$ given all our observation up until this point is captured by ${\alpha }_t(i)$. The likelihood that we end up in state $S_j$ at time $t+1$ knowing all our observation after this point is captured by ${\beta }_{t+1}(j)$.

Now that we know the probability of being in state $i$ and $j$, we just need to tie them together by multiplying it by the transition probability from state $i$ to $j$, and the probability of being in state $j$ given our observation at time $t+1$ :

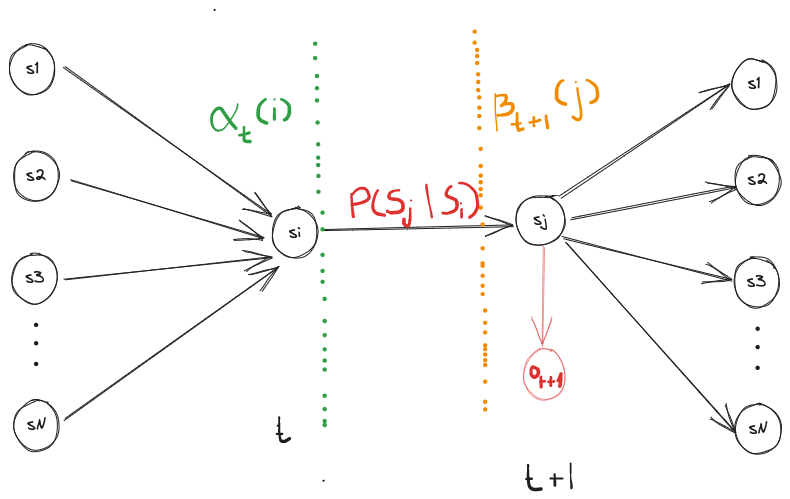
We can rewrite $\xi$ as:

$$\begin{array}{rl}\xi (i,j)=& P(q_t=S_i,q_{t+1}=S_j|O,\lambda )\\ & =\frac{{\alpha }_t(i)P(S_j|S_i)P(O_{t+1}|S_j){\beta }_{t+1}(j)}{P(O|\lambda )}\\ & =\frac{{\alpha }_t(i)P(S_j|S_i)P(O_{t+1}|S_j){\beta }_{t+1}(j)}{{\sum }_{i=1}^N{\sum }_{j=1}^N{\alpha }_t(i)P(S_j|S_i)P(O_{t+1}|S_j){\beta }_{t+1}(j)}\end{array}$$

Note that we divide by $P(O|\lambda )$ to normalize our likelihood because we are looking for probabilities.

We can write the probability of being in state $i$ at time $t$ as:

$${\gamma }_t(i)=\sum _{j=1}^N\xi (i,j)$$

Now we have:

$$\sum _{t=1}^T{\gamma }_t(i)=expectednumberoftransitionsfrom{S}_i$$

and

$$\sum _{t=1}^T{\xi }_t(i,j)=expectednumberoftransitionsfrom{S}_{i}to{S}_j$$

Now we can update our parameters.

To update our stationary distribution:

$$\pi ={\gamma }_1(i):expectedfrequencyof{S}_{i}attimet=1$$

To update our transition matrix:

$$\begin{array}{rl}{\overline{a}}_{ij}=& \frac{expectednumberoftransitionsfrom{S}_{i}to{S}_j}{expectednumberoftransitionsfrom{S}_i}\\ & =\frac{{\sum }_{t=1}^{T-1}{\xi }_t(i,j)}{{\sum }_{t=1}^{T-1}{\gamma }_t(i)}\end{array}$$

To update our emission probabilities:

$$\begin{array}{rl}{\overline{b}}_j=& \frac{expectednumberoftimeinstatejandobserving{v}_k}{expectednumberoftimeinstatej}\\ & =\frac{{\sum }_{t=1}^T{\gamma }_t(j)s.t.O_t=v_k}{{\sum }_{t=1}^T{\gamma }_t(j)}\end{array}$$

*Note $s.t{O}_t=v_k$ means such that observation at time $t$ is $v_k$, we only sum terms that meets this condition.

Further Readings:

• Baum-Welch Algorithm
• Principles of Autonomy and Decision Making
• A Tutorial on Hidden Markov Models and Selected Applications in Speech recognition
• Hidden Markov Models 12: the Baum-Welch algorithm