Forward Algorithm

#maths Given a Hidden Markov Model with known parameters (stationary distribution/ transition probability/ emission probability) we can calculate the likelihood of seeing a sequence observations, efficiently using the forward algorithm.

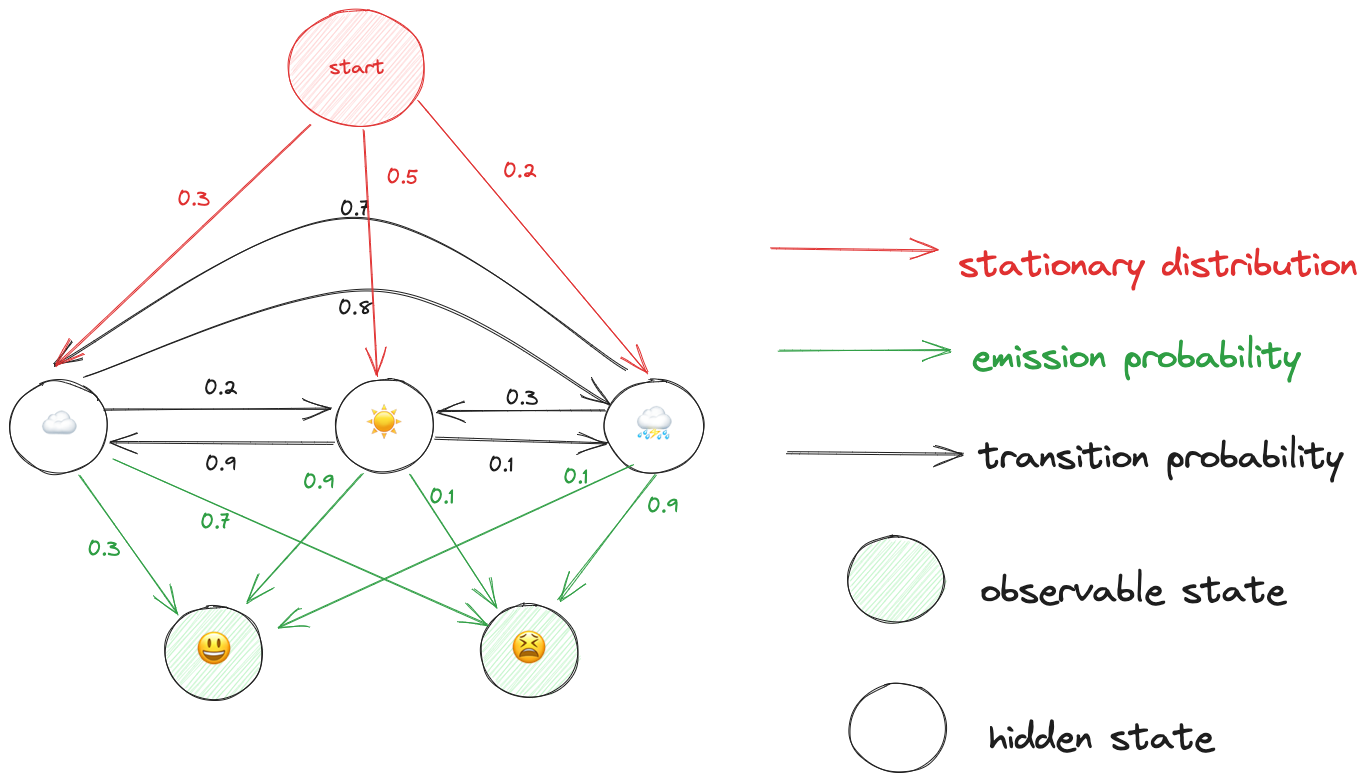
Let’s say we observe 😫,😃. What is the likelihood of observing these states, given our hidden markov model?

The naive approach is to enumerate all possible hidden states and sum their probabilities. That is:

$P(O)={\sum }_{\forall q}P(O|q)P(q)$ Where:

• $q=q_1,q_2,\dots ,q_T$ represents a sequence of states through the HMM that generates the observations $O$.
• $P(O|q)$ is the probability of observing the sequence $O$ given the state sequence $q$, which is the product of the observation probabilities for each observed symbol at each step in the sequence given the state at that step: ${\prod }_{t=1}^{T}P(o_t|q_t)$.
• $P(q)$ is the probability of the state sequence $q$, which includes the initial state probability and the product of the transition probabilities for each transition in the sequence: $P(q_1){\prod }_{t=1}^{T-1}P(q_{t+1}|q_t)$.
• The sum is taken over all possible sequences of states $q$ of length $T$.

We can expand the equation to:

$P(O)={\sum }_{\forall q}[({\prod }_{t=1}^{T}P(o_t|q_t))\ast (P(q_1){\prod }_{t=1}^{T-1}P(q_{t+1}|q_t))]$ For $O=\{😫,😃\}$ the permutations of states $q$ that can give rise to $O$ are

$$q=\{\{☀\stackrel{◯}{R},☀\stackrel{◯}{R}\},\{☀\stackrel{◯}{R},☁\stackrel{◯}{R}\},\{☀\stackrel{◯}{R},⛈\},\{☁\stackrel{◯}{R},☀\stackrel{◯}{R}\},\{☁\stackrel{◯}{R},☁\stackrel{◯}{R}\},\{☁\stackrel{◯}{R},⛈\},\{⛈,☀\stackrel{◯}{R}\},\{⛈,☁\stackrel{◯}{R}\},\{⛈,⛈\}\}$$

The number of possible hidden states can be calculated with:

$$P(n,r)=n^r$$

where $n$ is the number of states and $r$ is the number of observations. This is an exponential function that grows with the number of observations we make.

The probability of making observation $O$ is:

$$\begin{array}{rl}P(O=\{o_1=😫,o_2=😃\})& =\sum _{\forall q}[(\prod _{t=1}^{T}P(o_t|q_t))\ast (P(q_1)\prod _{t=1}^{T-1}P(q_{t+1}|q_t))]\\ & =\sum _{\forall q}P(q_1)\ast P(o_1|q_1)\ast P(q_2|q_1)\ast P(o_2|q_2)\\ & =\sum _{\forall q}P(q_1)\ast P(😫|q_1)\ast P(q_2|q_1)\ast P(😃|q_2)\\ & =P(☀\stackrel{◯}{R})\ast P(😫|☀\stackrel{◯}{R})\ast P(☀\stackrel{◯}{R}|☀\stackrel{◯}{R})\ast P(😃|☀\stackrel{◯}{R})\\ & +P(☀\stackrel{◯}{R})\ast P(😫|☀\stackrel{◯}{R})\ast P(☁\stackrel{◯}{R}|☀\stackrel{◯}{R})\ast P(😃|☁\stackrel{◯}{R})\\ & +P(☀\stackrel{◯}{R})\ast P(😫|☀\stackrel{◯}{R})\ast P(⛈|☀\stackrel{◯}{R})\ast P(😃|⛈)\\ & +P(☁\stackrel{◯}{R})\ast P(😫|☁\stackrel{◯}{R})\ast P(☀\stackrel{◯}{R}|☁\stackrel{◯}{R})\ast P(😃|☀\stackrel{◯}{R})\\ & +P(☁\stackrel{◯}{R})\ast P(😫|☁\stackrel{◯}{R})\ast P(☁\stackrel{◯}{R}|☁\stackrel{◯}{R})\ast P(😃|☁\stackrel{◯}{R})\\ & +P(☁\stackrel{◯}{R})\ast P(😫|☁\stackrel{◯}{R})\ast P(⛈|☁\stackrel{◯}{R})\ast P(😃|⛈)\\ & +P(⛈)\ast P(😫|⛈)\ast P(☀\stackrel{◯}{R}|⛈)\ast P(😃|☀\stackrel{◯}{R})\\ & +P(⛈)\ast P(😫|⛈)\ast P(☁\stackrel{◯}{R}|⛈)\ast P(😃|☁\stackrel{◯}{R})\\ & +P(⛈)\ast P(😫|⛈)\ast P(⛈|⛈)\ast P(😃|⛈)\end{array}$$

Writing it out we can see that we are recomputing certain parts of the equation. For example $P(⛈)\ast P(😫|⛈)$ is computed 3 times. We can make the computation of $P(O)$ much more efficient by computing it recursively. This is where the forward algorithm comes in.

$$\begin{array}{rlr}\text{Initialization:}& {\alpha }_1(X_i)=\pi [i]P(Y^0|X_i),& 1\le i\le N\\ \text{Recursion:}& {\alpha }_{t+1}(i)=[\sum _{j=1}^N{\alpha }_t(X_j)P(X_i|X_j)]P(Y^t|X_i),& 1\le t\le T-1,1\le i\le N\\ \text{Termination:}& P(O)=\sum _{i=1}^N{\alpha }_T(i),& \end{array}$$

Let’s recompute our example using the forward algorithm:

$$\begin{array}{rl}\underline{Initialization:}& \\ & \\ t=1:& {\alpha }_1(☀\stackrel{◯}{R})=\pi [☀\stackrel{◯}{R}]P(😫|☀\stackrel{◯}{R}),\\ & {\alpha }_1(☁\stackrel{◯}{R})=\pi [☁\stackrel{◯}{R}]P(😫|☁\stackrel{◯}{R}),\\ & {\alpha }_1(⛈)=\pi [⛈]P(😫|⛈)\\ & \\ \underline{Recursion:}& \\ & \\ t=2:& {\alpha }_2(☀\stackrel{◯}{R})=[{\alpha }_1(☀\stackrel{◯}{R})P(☀\stackrel{◯}{R}|☀\stackrel{◯}{R})+{\alpha }_1(☁\stackrel{◯}{R})P(☀\stackrel{◯}{R}|☁\stackrel{◯}{R})+{\alpha }_1(⛈)P(☀\stackrel{◯}{R}|⛈)]P(😃|☀\stackrel{◯}{R})\\ & {\alpha }_2(☁\stackrel{◯}{R})=[{\alpha }_1(☀\stackrel{◯}{R})P(☁\stackrel{◯}{R}|☀\stackrel{◯}{R})+{\alpha }_1(☁\stackrel{◯}{R})P(☁\stackrel{◯}{R}|☁\stackrel{◯}{R})+{\alpha }_1(⛈)P(☁\stackrel{◯}{R}|⛈)]P(😃|☁\stackrel{◯}{R})\\ & {\alpha }_2(⛈)=[{\alpha }_1(☀\stackrel{◯}{R})P(⛈|☀\stackrel{◯}{R})+{\alpha }_1(☁\stackrel{◯}{R})P(⛈|☁\stackrel{◯}{R})+{\alpha }_1(⛈)P(⛈|⛈)]P(😃|⛈)\\ & \\ \underline{Termination:}& \\ & \\ P(O)=& {\alpha }_2(☀\stackrel{◯}{R})+{\alpha }_2(☁\stackrel{◯}{R})+{\alpha }_2(⛈)\end{array}$$

The complexity to compute the forward algorithm is $O(N^{2}T)$. This is because for each of the observations $T$, we compute the transition from each state to every other state leading to $N\ast N$.

In comparison the complexity for the naive approach is $O(N^T)$, which is infeasible for even moderate sized $T$.

Further Reading:

• Forward Algorithm Clearly Explained | Hidden Markov Model | Part - 6